Author Donald Ahrens in his text Meteorology Today
describes a rainbow
as "one of the most spectacular light shows observed on earth". Indeed
the traditional rainbow is sunlight spread out into its spectrum of colors
and diverted to the eye of the observer by water droplets.
The "bow" part of the word describes the fact that the rainbow is a group of
nearly circular arcs of color all having a common center.
He writes:"Considering that this bow appears not only in the sky, but also in the air near us, whenever there are drops of water illuminated by the sun, as we can see in certain fountains, I readily decided that it arose only from the way in which the rays of light act on these drops and pass from them to our eyes. Further, knowing that the drops are round, as has been formerly proved, and seeing that whether they are larger or smaller, the appearance of the bow is not changed in any way, I had the idea of making a very large one, so that I could examine it better.
Descarte describes how he held up a large sphere in the sunlight and looked at
the sunlight reflected in it. He wrote "I found that if the sunlight
came, for example, from the part of the sky which is marked AFZ
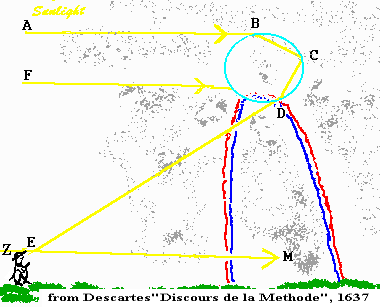
and my eye was at the point E, when I put the globe in position BCD, its part D appeared all red, and much more brilliant than the rest of it; and that whether I approached it or receded from it, or put it on my right or my left, or even turned it round about my head, provided that the line DE always made an angle of about forty-two degrees with the line EM, which we are to think of as drawn from the center of the sun to the eye, the part D appeared always similarly red; but that as soon as I made this angle DEM even a little larger, the red color disappeared; and if I made the angle a little smaller, the color did not disappear all at once, but divided itself first as if into two parts, less brilliant, and in which I could see yellow, blue, and other colors ... When I examined more particularly, in the globe BCD, what it was which made the part D appear red, I found that it was the rays of the sun which, coming from A to B, bend on entering the water at the point B, and to pass to C, where they are reflected to D, and bending there again as they pass out of the water, proceed to the point ".
This quotation illustrates how the shape of the rainbow is explained. To simplify the analysis, consider the path of a ray of monochromatic light through a single spherical raindrop. Imagine how light is refracted as it enters the raindrop, then how it is reflected by the internal, curved, mirror-like surface of the raindrop, and finally how it is refracted as it emerges from the drop. If we then apply the results for a single raindrop to a whole collection of raindrops in the sky, we can visualize the shape of the bow.
The traditional diagram to illustrate this is shown here as adapted from
Humphreys, Physics of the Air. 
It represents the path of one light ray incident on a water droplet from the
direction SA. As the light beam enters the surface of the drop at A, it
is bent (refracted)
a
little and strikes the inside wall of the drop
at B, where it is reflected back to C. As it emerges from the drop it is
refracted (bent) again into the direction CE. The angle D represents a
measure of the deviation of the emergent ray from its original direction.
Descartes calculated this deviation for a ray of red light to be about
180 - 42 or 138 degrees.
The ray drawn here is significant because it represents the ray that has the smallest angle of deviation of all the rays incident upon the raindrop. It is called the Descarte or rainbow ray and much of the sunlight as it is refracted and reflected through the raindrop is focused along this ray. Thus the reflected light is diffuse and weaker except near the direction of this rainbow ray. It is this concentration of rays near the minimum deviation that gives rise to the arc of rainbow.
The sun is so far away that we can, to a good approximation, assume that sunlight can be represented by a set of parallel rays all falling on the water globule and being refracted, reflected internally, and refracted again on emergence from the droplet in a manner like the figure. Descartes writes
I took my pen and made an accurate calculation of the paths of the rays which fall on the different points of a globe of water to determine at which angles, after two refractions and one or two reflections they will come to the eye, and I then found that after one reflection and two refractions there are many more rays which can be seen at an angle of from forty-one to forty-two degrees than at any smaller angle; and that there are none which can be seen at a larger angle" (the angle he is referring to is 180 - D).
A typical raindrop is spherical and therefore its effect on sunlight is symmetrical about an axis through the center of the drop and the source of light (in this case the sun). Because of this symmetry, the two-dimensional illustration of the figure serves us well and the complete picture can be visualized by rotating the two dimensional illustration about the axis of symmetry. The symmetry of the focusing effect of each drop is such that whenever we view a raindrop along the line of sight defined by the rainbow ray, we will see a bright spot of reflected/refracted sunlight. Referring to the figure, we see that the rainbow ray for red light makes an angle of 42 degrees between the direction of the incident sunlight and the line of sight. Therefore, as long as the raindrop is viewed along a line of sight that makes this angle with the direction of incident light, we will see a brightening. The rainbow is thus a circle of angular radius 42 degrees, centered on the antisolar point, as shown schematically here.
We don't see a full circle because the earth gets in the way. The lower the sun is to the horizon, the more of the circle we see -right at sunset, we would see a full semicircle of the rainbow with the top of the arch 42 degrees above the horizon. The higher the sun is in the sky, the smaller is the arch of the rainbow above the horizon.
The colors of the rainbow arise from two basic facts:
This implies that when we see a rainbow and its band of colors we are
looking at light refracted and reflected from different raindrops,
some viewed at an angle of 42 degrees; some, at an angle of 40 degrees, and
some in between. This is illustrated in this drawing,
adapted from Johnson's Physical Meteorology. This rainbow of two
colors would have a width of almost 2 degrees (about four times larger
than the angular size as the full moon). Note that even though
blue light is refracted more than red light in a single drop, we see the
blue light on the inner part of the arc because we are looking along a
different line of sight that has a smaller angle (40 degrees) for the blue.
It is possible for light to be reflected more than twice within a raindrop, and one can calculate where the higher order rainbows might be seen; but these are never seen in normal circumstances.
The "purity" of the colors of the rainbow depends on the size of the raindrops. Large drops (diameters of a few millimeters) give bright rainbows with well defined colors; small droplets (diameters of about 0.01 mm) produce rainbows of overlapping colors that appear nearly white. And remember that the models that predict a rainbow arc all assume spherical shapes for raindrops.
There is never a single size for water drops in rain but a mixture of many sizes and shapes. This results in a composite rainbow. Raindrops generally don't "grow" to radii larger than about 0.5 cm without breaking up because of collisions with other raindrops, although occasionally drops a few millimeters larger in radius have been observed when there are very few drops (and so few collisions between the drops) in a rainstorm. Bill Livingston suggests: " If you are brave enough, look up during a thunder shower at the falling drops. Some may hit your eye (or glasses), but this is not fatal. You will actually see that the drops are distorted and are oscillating."
It is the surface tension of water that moulds raindrops into spherical shapes, if no other forces are acting on them. But as a drop falls in the air, the 'drag' causes a distortion in its shape, making it somewhat flattened. Deviations from a spherical shape have been measured by suspending drops in the air stream of a vertical wind tunnel (Pruppacher and Beard, 1970, and Pruppacher and Pitter, 1971). Small drops of radius less than 140 microns (0.014 cm) remain spherical, but as the size of the drop increases, the flattening becomes noticeable. For drops with a radius near 0.14 cm, the height/width ratio is 0.85. This flattening increases for larger drops.
Spherical drops produce symmetrical rainbows, but rainbows seen when the sun is near the horizon are often observed to be brighter at their sides, the vertical part, than at their top. Alistair Fraser has explained this phenomenon as resulting from the complex mixture of size and shape of the raindrops. The reflection and refraction of light from a flattened water droplet is not symmetrical. For a flattened drop, some of the rainbow ray is lost at top and bottom of the drop. Therefore, we see the rays from these flattened drops only as we view them horizontally; thus the rainbow produced by the large drops is is bright at its base. Near the top of the arc only small spherical drops produce the fainter rainbow.
The meteorological discussion Humphreys presents is appropriate for the northern temperate zones that have a prevailing wind, and also for a normal diurnal change in the weather.
In Minnaert's excellent book Light and Colour in the Open Air you can find a number of experiments on how to study the nature of rainbows. Here is an illustration of one of his suggestions. Other demonstration projects are listed here .
Another classroom example is found here. Meg Beal, while a seventh-grader, prepared a science fair project that illustrated the nature of rainbows. The Beal family provided a photograph (1MB) of her excellent demonstration.
For those wanting to try to demonstrate the nature of a rainbow in a classroom, here are examples.
I am indebted to William C. Livingston, astronomer at the National Optical Astronomy Observatory in Tucson Arizona for his expert assistance in preparing this paper, and to Seth Sharpless for his critical reading of the manuscript. Charles A. Knight, an expert on rain at the National Center for Atmospheric Physics, provided valuable guidance on the interesting properties of raindrops.
You are the 46739th visitor to "About Rainbows" since 19 September 1995, hope you enjoyed it!
blynds@unidata.ucar.edu
